One Level Higher
(Professor Quirrell had remarked over their lunch that Harry really needed to conceal his state of mind better than putting on a blank face when someone discussed a dangerous topic, and had explained about one-level deceptions, two-level deceptions, and so on. So either Severus was in fact modeling Harry as a one-level player, which made Severus himself two-level, and Harry’s three-level move had been successful; or Severus was a four-level player and wanted Harry to think the deception had been successful. Harry, smiling, had asked Professor Quirrell what level he played at, and Professor Quirrell, also smiling, had responded, One level higher than you.)
― Eliezer Yudkowsky, Harry Potter and the Methods of Rationality (Chapter 27: Empathy)
A Keynesian beauty contest is a hypothetical beauty contest in which the judges pick, not whom they personally find most attractive, but whom they expect other judges to pick. In such a contest, we can imagine several different levels that a judge can operate on. A judge who selects who they find most attractive is a Level 0 player. A judge who selects who they think others find most attractive is a Level 1 player. A judge who selects who they think other judges think other judges find most attractive is a Level 2 player. And so on. Such thinking is called level-k reasoning.
Crucially, judges wish to be exactly one level higher than the other judges. If everyone is playing at Level 0, you don’t want to operate at Level 2; you want to be at Level 1. This leads to a natural question: how many levels do people usually play out, and is there a practical limit?
Guess 2/3 of the average
“Guess 2/3 of the average” is a game that clarifies the concept. Each player names a real number between 0 and 100, inclusive. The winner is the player who chose the number closest to 2/3 of the mean of the guesses (hence the name). Such a game lends itself naturally to level-k reasoning.
- A population of Level 0 players can be modeled as making random uniformly distributed guesses, yielding a mean guess of 50.
- A population of Level 1 players, each of them assuming everyone else is a Level 0 player, will guess 2/3 of the predicted mean (50), yielding a mean guess of 33.3.
- A population of Level 2 players, each of them assuming everyone else is a Level 1 player, will guess 2/3 of the predicted mean (33.3), yielding a mean guess of 22.2.
- And so on.
From the average guess, we can compute the level the population is playing at, using the following equation: $f(x) = \log_{\frac{2}{3}} \left(\frac{x}{50}\right)$. The equation yields negative values for average guesses over 50, but those can be interpreted as irrationality, a sort of negative rationality, at least if we assume the levels measure rationality. This is not so far-fetched, as Level-$\infty$ reasoning share similarities to the concept of superrationality. This mapping makes the population’s implicit level measurable from the mean guess.
Paper: Unraveling in Guessing Games: An Experimental Study
In this paper, the author runs multiple experiments where participants play “guess $p$ of the average”, with $p$ can equal $\frac{1}{2}$, $\frac{2}{3}$, or $\frac{4}{3}$. In each of these games, participants select a number between 0 and 100, inclusive, and the winner is the person who selected the number closest to $p$ multiplied by the mean of the guesses.
For $0 \leq p < 1$, there exists only one Nash equilibrium: when all players choose 0. For $p = 1$, the game is a coordination game, and there are infinitely many equilibrium points. For $p > 1$ and $2p < M$ (where $M$ is the number of players), there are two equilibrium points: everyone choosing 0 and everyone choosing 100 (however, it seems reasonable to predict that typical populations of humans will tend towards the equilibrium of choosing 100).
For the first rounds of each experiment, we can view the mean guesses as the population level. The median guesses tell us the level of the median player.
- $p = \frac{1}{2}$: The mean guess was 27.05 (population Level 0.9) and the median was 17 (median level 1.6).
- $p = \frac{2}{3}$: The mean guess was 36.73 (population Level 0.8) and the median was 33 (median level 1).
- $p = \frac{4}{3}$: The mean guess was 60.12 (population Level 0.6) and the median was 66 (median level 1).
We might also want to know the distribution of player levels. The paper splits guesses into those that fall into neighborhood intervals (corresponding with the discrete levels), and those falling into interim intervals (between the neighborhood intervals).
- $p = \frac{1}{2}$
- 16% of players were Level 0, 21% were Level 1, 29% were Level 2, and 4% were Level 3.
- 6% of players guessed above the mean, 4% were in between Levels 0 and 1, 10% were in between Levels 1 and 2, 8% were in between Levels 2 and 3, and 2% were higher than Level 3.
- $p = \frac{2}{3}$
- 7% of players were Level 0, 27% were Level 1, 24% were Level 2, and 1% were Level 3.
- 19% of players guessed above the mean, 6% were in between Levels 0 and 1, 3% were in between Levels 1 and 2, 4% were between Levels 2 and 3, and 7% were higher than Level 3.
- $p = \frac{4}{3}$
- 2% of players were Level 0, 29% were Level 1, 10% were Level 2, and 8% were Level 3.
- 27% of players guessed below the mean, 12% were in between Levels 0 and 1, 12% were in between Levels 1 and 2, and 0% were in between Levels 2 and 3. It was not possible for guesses to be higher than Level 3.
Since there are multiple rounds per experiment session, we can see how the mean/median level changes as the game repeats.
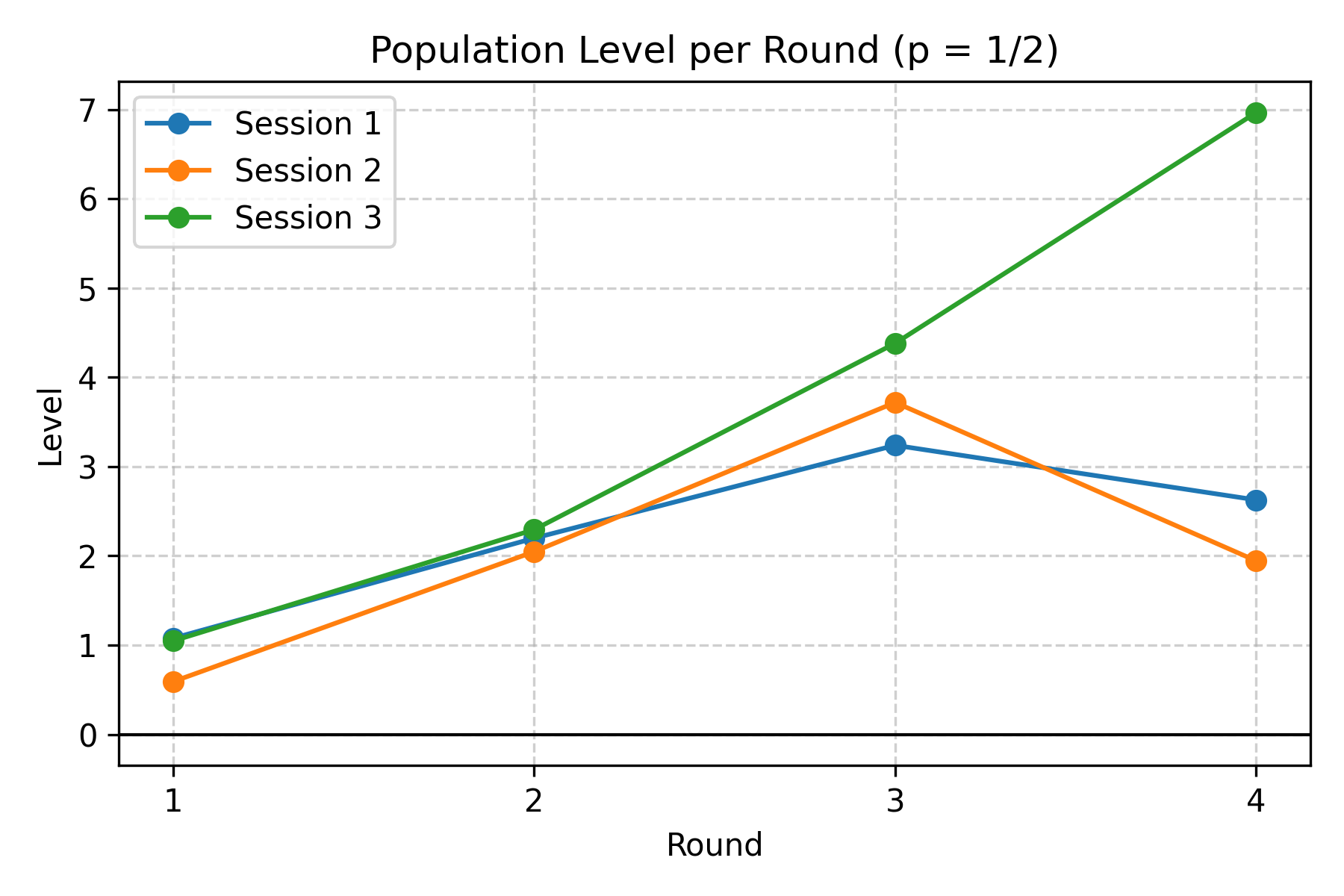
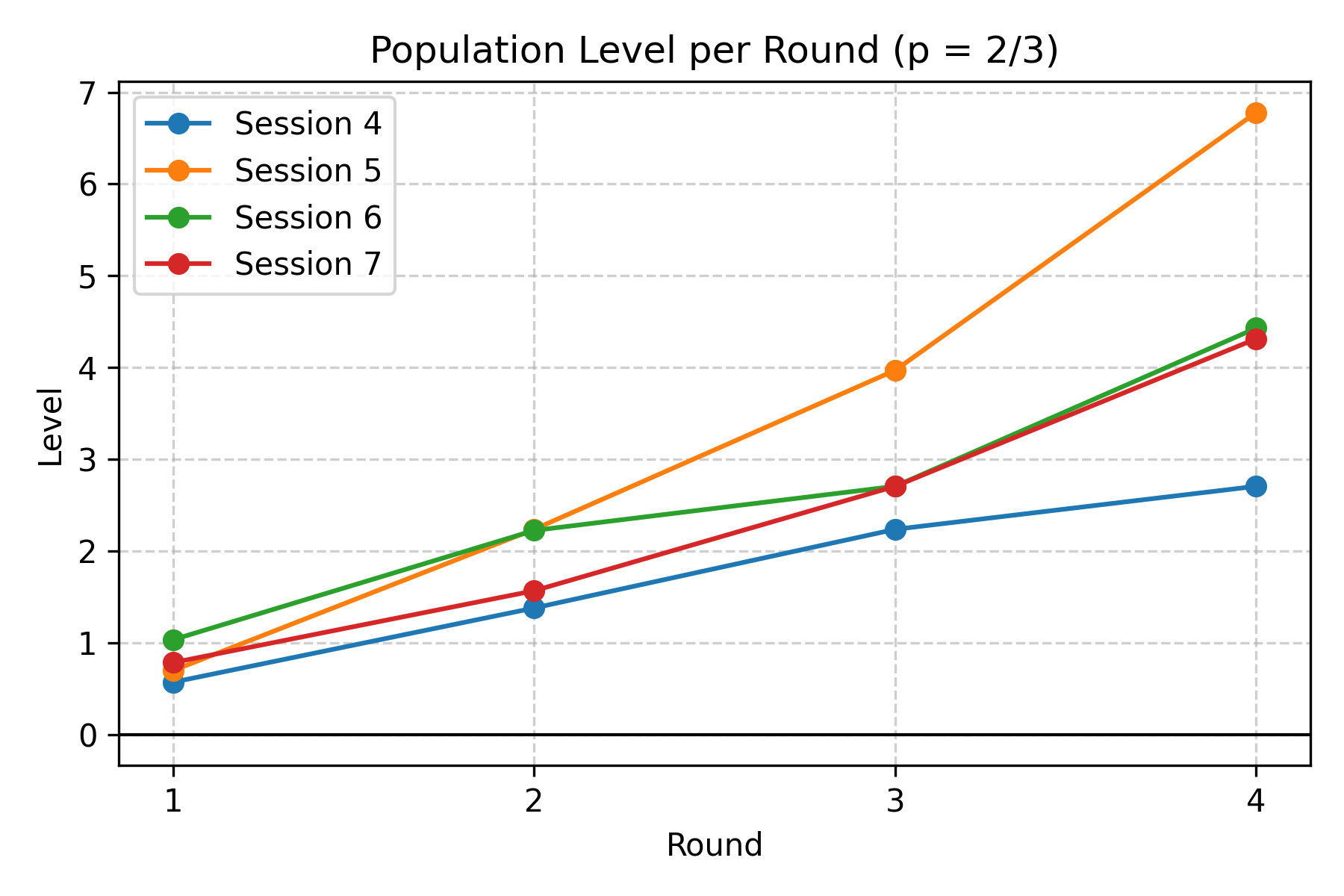
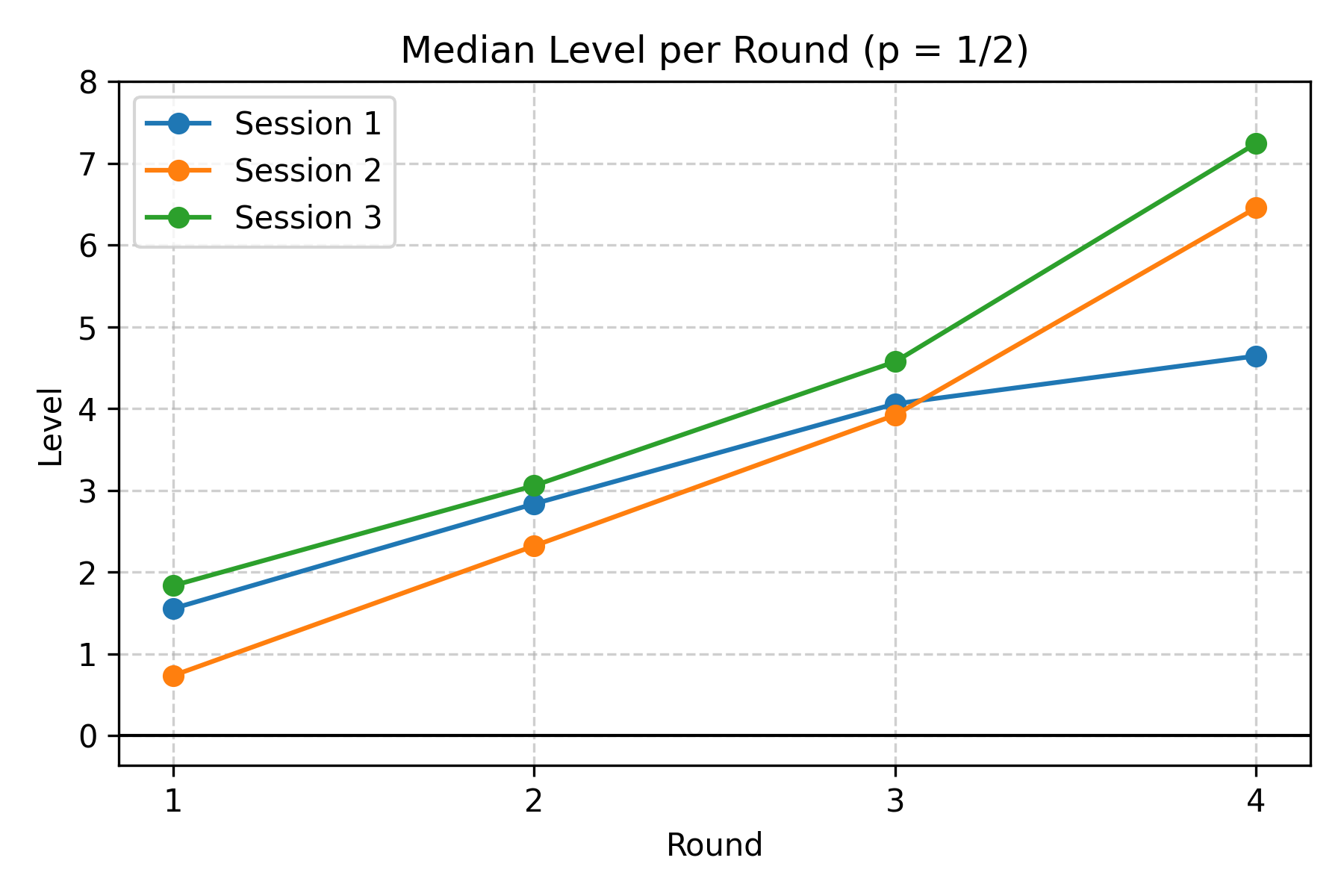
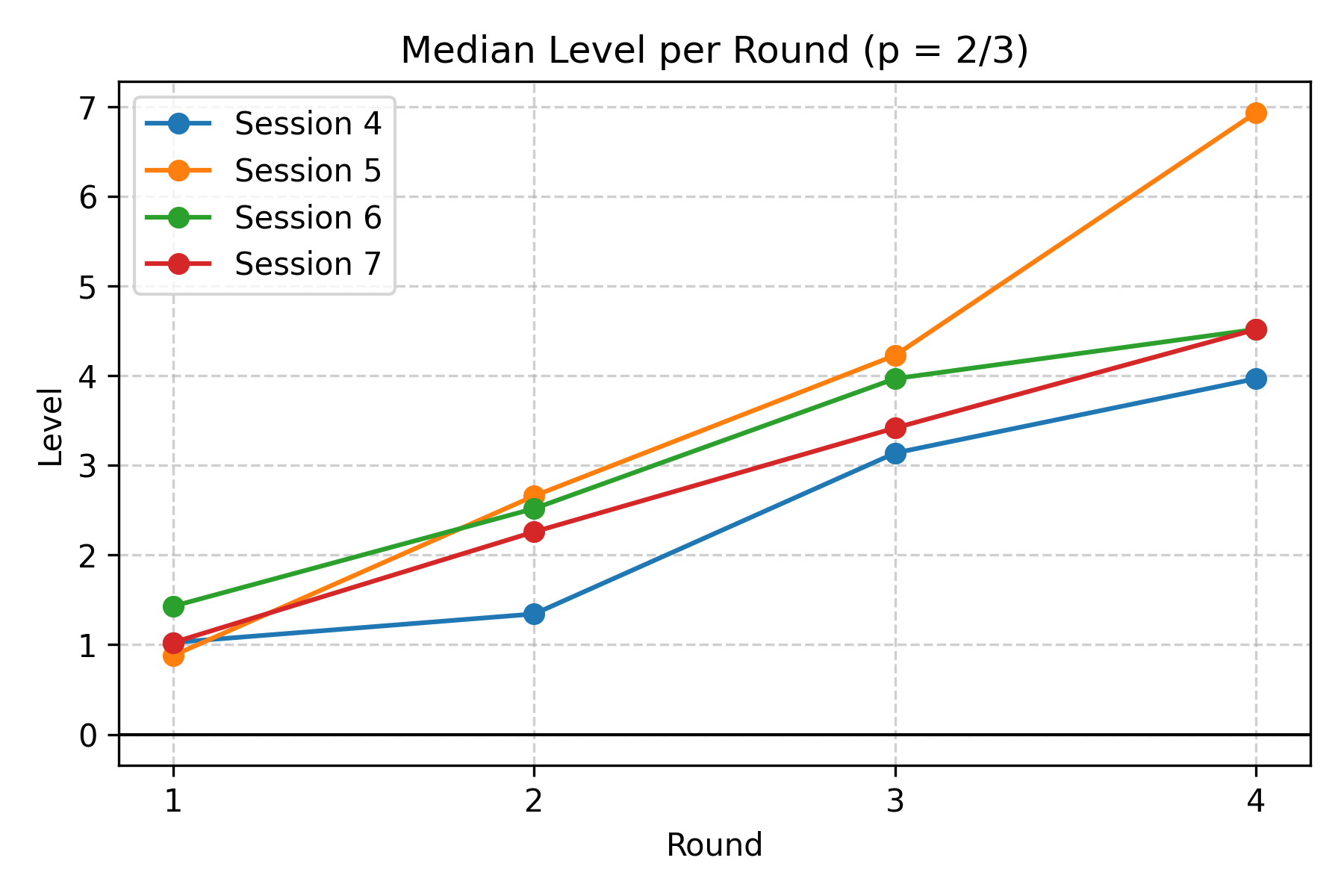
For a more fine-grained analysis, we can look at the distribution of how each person adjusts their level from round to round. In the following data, the authors classify the data of each of the subsequent periods according to the reference point ($r$, the mean of the previous period, not necessarily Period 1) and iteration steps (where step $n$ indicates a guess of $r\cdot p^n$). Guesses above the previous-period mean are aggregated into “Above mean₋₁”.
| Classification | Period 2 | Period 3 | Period 4 |
|---|---|---|---|
| Sessions 1–3 (p = 1/2) | |||
| Higher steps | 4.2% | 4.2% | 20.8% |
| Step 3 | 25.0% | 12.5% | 22.9% |
| Step 2 | 31.3% | 60.4% | 29.2% |
| Step 1 | 27.0% | 12.5% | 14.5% |
| Step 0 | 2.1% | 4.1% | 4.2% |
| Above mean₋₁ | 10.4% | 6.3% | 8.3% |
| Sessions 4–7 (p = 2/3) | |||
| Higher steps | 7.5% | 1.5% | 7.5% |
| Step 3 | 11.9% | 17.9% | 25.3% |
| Step 2 | 31.3% | 46.2% | 47.8% |
| Step 1 | 20.9% | 16.4% | 10.4% |
| Step 0 | 14.9% | 7.5% | 3.0% |
| Above mean₋₁ | 13.4% | 10.5% | 6.0% |
Two clear patterns emerge. First, most people start near Level 1: Level 1 and Level 2 together typically account for the plurality of guesses. Second, repetition moves players upwards. Across rounds the median player typically advances about one level from round 1 to round 2, another 1–2 levels by round 3, and another 1–3 levels by round 4 in many sessions. The move toward higher levels is not uniform: a persistent minority make irrational or non-updating choices, but the modal behavior is updating towards higher levels.
Paper: Bounded rationality in Keynesian beauty contests: a lesson for central bankers?
Table 1 of this paper summarizes Keynesian beauty contests experiments from various studies.
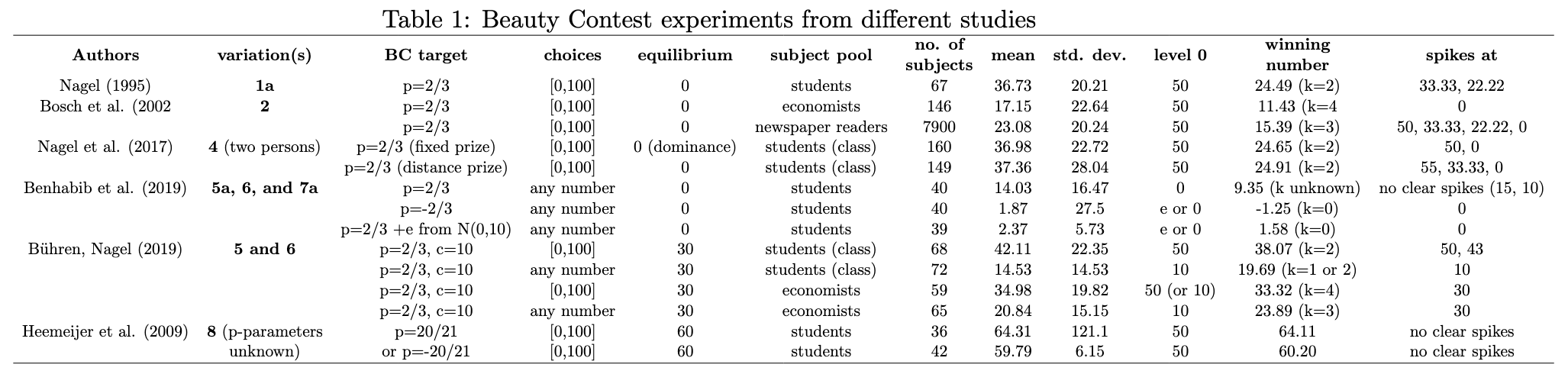
Generally, students (initially) operate at Level 1 while economists (initially) operate at Levels 2-3.
Yudkowsky’s Law of Ultrafinite Recursion
Level-k reasoning is closely related to the idea of recursion. A Level 0 player thinks. A Level 1 player thinks about what others think. A Level 2 player thinks about what others think others think. And so on. A limit to recursion would imply a limit to level-k reasoning. Eliezer Yudkowsky provides such a limit with his eponymous Yudkowsky’s Law of Ultrafinite Recursion, which states “In practice, infinite recursions are at most three levels deep.” The three levels are: Level 0 (base level), Level 1 (meta level), and Level 2 (meta-meta level). Examples of his law include:
- Bob thinks about “What does Alice think about Bob?” (Level 1; meta level) and on rare occasions “What does Alice think Bob thinks about Alice?” (Level 2; meta-meta level) but will not organically reason “What does Alice think Bob thinks about Alice’s model of Bob?” (Level 3; meta-meta-level).
- There’s a useful distinction between object-level reasoning (Level 0) and meta-level reasoning (Level 1), and very rarely it’s good to engage in meta-meta-reasoning (Level 2), but no good has ever come of meta-meta-meta anything (Level 3).
- A philosopher talking about qualia will say, “Consciousness is infinitely reflective. When I see a red object, I’m not only aware of redness itself (Level 0), but aware that I’m aware of the redness (Level 1), aware of being aware of my awareness (Level 2), and so on.”
- There can be agents (Level 0; one who works for an organization A), double agents (Level 1; one who pretends to work for organization B, but is in fact loyal to organization A), and triple agents (Level 2; one who pretends to work for organization A on behalf of organization B, but is in reality loyal to organization A). However, there are no quadruple agents (Level 3; I leave this to the reader’s imagination).
Yudkowsky offers the caveat that his Law applies “only to recursions that can go on forever. If there’s a recursion that can only go on for 65,536 levels in principle, it’s allowed to go 65,536 levels deep in practice. This is why chess-playing algorithms can extrapolate a game tree through more than three plies.” The claim isn’t that deep recursion is impossible. Rather, for ordinary humans engaging in ordinary reasoning, more than three levels rarely appear and rarely add useful insights.
We can look to sources outside of Yudkowsky to investigate the applicability of the Law of Ultrafinite Recursion.
What You (Want To)* Want
In Paul Graham’s essay, What You (Want To)* Want, he discusses three kinds of wants:
- Level 0: You want. (e.g., ‘I like classical music’)
- Level 1: You want to want. (e.g., ‘I want to like classical music’)
- Level 2: You want to want to want. (e.g., ‘I want to not want to like classical music’)
While he leaves the door open for an increasing tower of “want to”s, he acknowledges that in practice, three or four “want to”s are usually enough.
Ars Longa, Vita Brevis
In Scott Alexander’s short story, Ars Longa, Vita Brevis, there’s a quote that perfectly matches Yudkowsky’s Law:
“You’re talking about an infinite regress”, I said, when I had finished the glass.
“Not infinite. Architects. Teachers. Teachers of teachers, but the art of teaching teaching is much the same as the art of teaching. Three levels is enough.”
There are architects (Level 0), teachers of architects (Level 1), and teachers of teachers of architects (Level 2). There’s no need for anything else.
Spies of the Mind
In Sirlin’s post, Spies of the Mind, they discuss the concept of yomi, the ability to anticipate what your opponent will do next. You can know what your opponent will do (Level 1; yomi layer 1), your opponent can know that you know what he’ll do (Level 2; yomi layer 2), and you can know that your opponent knows that you know what he’ll do (Level 3; yomi layer 3). As for the next yomi layer? Sirlin asserts that there need only be 3 yomi layers, and that the yomi layer 4 loops back to layer 0. He provides a concrete example:
Let’s say I have a move (we’ll call it “m”) that’s really, really good. I want to do it all the time. (Here’s where the inequality of risk/reward comes in. If all my moves are equally good, this whole thing falls apart.) The “Level 0” case here is discovering how good that move is and doing it all the time. Then, you will catch on and know that I’m likely to do that move a lot (yomi layer 1), so you’ll need a counter move (we’ll call it “c1”). You’ve stopped me from doing m. You’ve shut me down. I need a way to stop you from doing c1. I need a counter to your counter, or “c2.”
Now you don’t know what to expect from me anymore. I might do m or I might do c2. Interestingly, I probably want to do m, but I just do c2 to scare you into not doing c1 anymore. Then I can sneak in more m.
You don’t have adequate choices yet. I can alternate between m and c2, but all you have is c1. You need a counter to c2, which we’ll call c3. Now we each have two moves.
Me: m, c2
You: c1, c3.Now I need a counter to c3. The tendency for game designers might be to create a c4 move, but it’s not necessary. The move m can serve as my c4. Basically, if you expect me to do my counter to your counter (rather than my original good move m), then I don’t need a counter for that; I can just go ahead and do the original move—if the game is designed that way. Basically, supporting moves up to yomi layer 3 is the minimum set of counters needed to have a complete set of options, assuming yomi layer 4 wraps around back to layer 0.
Conclusion
For the strategic player, aiming to always be one (and only one) step ahead of their opponents, there are practical insights. The average person operates at Level 1, with Level 2 also being common, and Level 3 being rare (unless one is playing against an opponent for whom meta-reasoning is assumed, such as an economist). Additional evidence from Eliezer Yudkowsky, Paul Graham, and Scott Alexander show that meta-reasoning above Level 2 does not come naturally to humans. Finally, when games are repeated, people tend to vary in their level of reasoning. Some will continue to make the best counter to your last move, while others will start to take into account that you may have taken their counter into account.