Epistemic Aggregation Methods

Modern societies rely on distributed judgment. Juries decide guilt, online users rate the credibility of news, and peer review relies on a community of scientists. A conceptual model of such epistemic aggregation methods is essential. It lets us ask precise questions: What properties make a crowd’s estimate more accurate than an individual’s? When do more participants help, and when do they amplify shared error? How can we design mechanisms that emphasize information rather than noise or ideology?

A useful starting point is looking at jury theorems. The simplest jury theorem is the Condorcet jury theorem, which formalizes how group accuracy depends on individual competence and independence. It provides a minimal model: if each voter is more likely than not to be correct, and their votes are independent, then the majority vote converges on the truth as the group grows. We can think of epistemic aggregation methods as those that either increase the influence of more competent participants or reduce correlated error.

Below are three examples.

Surprisingly Popular Elicitation Technique

For a given question, ask respondents two questions about every candidate answer:

1. “What is your probability that this answer is correct?” (the right question)
2. “What probability will the average respondent assign to this answer?” (the popular question)

For each candidate answer, compute:

surprise_gap = average(right) − average(popular)

Choose the answer with the largest positive surprise_gap. The reason why this works is simple: when knowledgeable respondents possess private evidence that others lack, they rate the correct answer higher than they expect the average respondent to rate it. That produces a positive gap for the correct answer and a smaller (or negative) gap for incorrect answers.

Example

Question: “Is Columbia the capital of South Carolina?”

• Average answer to right question: Yes 75%, No 25%
• Average answer to popular question: Yes 55%, No 45%
• Gaps: Yes 20% (75 − 55), No −20% (25 − 45) → choose Yes.

Caveats

If experts systematically don’t have a good gauge of public opinion, or if there are no experts, then this technique produces less accurate answers.

Excluding Rounders

When a survey asks for a numerical estimate (e.g., “what percentage of residents were born abroad?”), many respondents answer with rounded numbers (multiples of 5 or 10). Rounded responses often signal guesswork¹. A study by the European University Institute examined this effect directly: respondents in several European countries were asked to estimate the percentage of foreign-born residents in their country.

Rounders (those who gave answers like 10%, 15%, etc) systematically overestimated the true foreign-born share by wide margins: usually 15 percentage points or more, and in one case by over 20 points. Non-rounders, those who provided more granular answers (such as 17% or 23%), were far more accurate: their mean estimates were typically within 5 percentage points of the official figures.

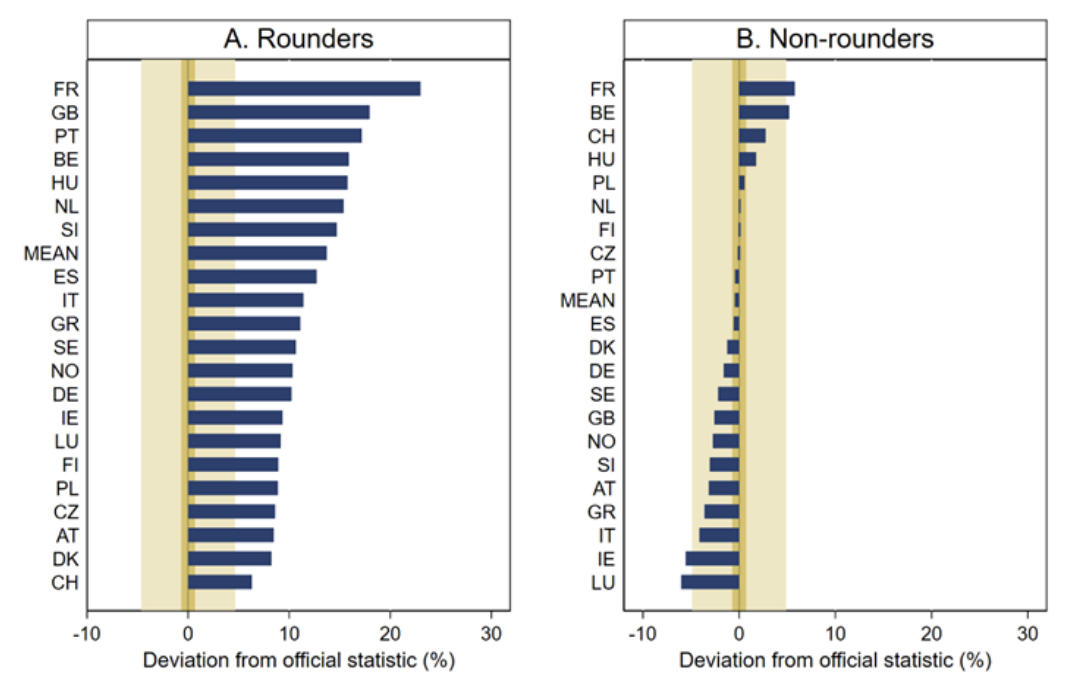
The probable explanation is simple: uninformed respondents choose a round number that sounds reasonable. Knowledgeable respondents use reference points (e.g., past statistics, comparative magnitudes) that generate more precise answers.

This suggests a simple rule: ignore rounders and use the average guess of non-rounders instead.

Caveats

Sometimes, the answer actually is a round number. Excluding rounders would mean excluding those who gave correct answers!

Community Notes

One of the components of the Community Notes algorithm is matrix factorization. Each rating of a note is predicted as

$ \hat{r}_{u,n} = \mu + i_u + i_n + f_u \cdot f_n $

where $\mu$ is the global intercept term, $i_u$ is the user’s intercept term, $i_n$ is the note’s intercept term, and $f_u$ and $f_n$ are the user’s and note’s factor vectors, respectively. When the user and note factor vectors are similar, a user is expected to give a higher rating to the note. In theory, the factor vectors account for the effect of a user’s viewpoint on how they rate different notes. In practice, Community Notes works surprisingly well for a crowd-sourced fact-checking algorithm, especially on Twitter of all platforms. The factor vectors can be interpreted as adjusting for ideological bias in users’ ratings, making the aggregate judgments depend more on factual accuracy than on viewpoint.